简要介绍
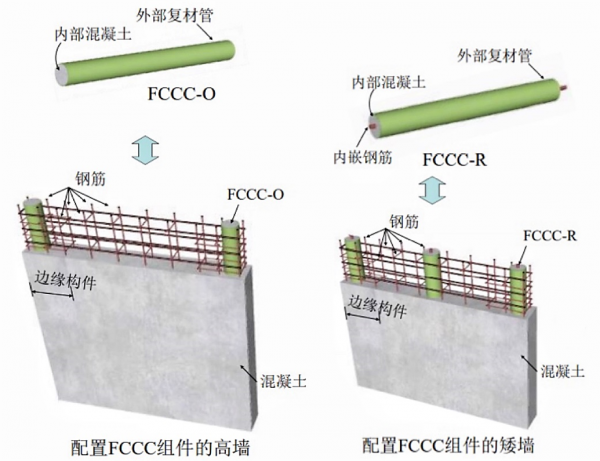
该工具箱用于计算内置复材约束芯柱的组合剪力墙的承载力,其构造如下图所示。对于高宽比大于2的高墙,主要发生弯曲破坏,基于平截面假定,考虑复材管约束混凝土压区合力作用的简化,提出正截面压弯承载力设计计算公式;对于高宽比为1的矮墙,主要发生剪切破坏,基于混凝土软化的拉压杆模型,提出抗剪承载力设计计算公式。
参考文献:
过镇海. 钢筋混凝土原理[M]. 北京: 清华大学出版社, 2012.
纤维增强复合材料建设工程应用技术与规范(GB 50608-2010) [S]. 北京: 中国计划出版社, 2010.
中华人民共和国建设部. JGJ3-2010. 高层建筑混凝土结构技术规程[S]. 北京: 中国建筑工业出版社, 2010.
CECS 188: 2005. 钢管混凝土叠合柱技术规程[S]. 北京: 中国计划出版社, 2002.
Hwang S J, and Lee H J. Analytical model for predicting shear strengths of interior reinforced concrete beam-column joints for seismic resistance[J]. ACI Structural Journal, 2000, 97(1):35-44.
Hwang S J, Lu W Y , and Lee H J. Shear strength prediction for deep beams[J]. ACI Structural Journal , 2000, 97(3):367-376.
Hwang S J, Lu W Y , and Lee H J. Shear strength prediction for reinforced concrete corbels[J]. ACI Structural Journal, 2000, 97(4):543-552.
Hwang S J, Fang W H, Lee H J, and Y u H W. Analytical model for predicting shear strength of squat walls[J]. Journal of Structural Engineering, 2001, 127(1):43-50.
Hwang S J and Lee H J. Strength prediction for discontinuity regions by softened strut-and-tie model[J]. Journal of Structural Engineering, 2002, 128(12):1519-1526.
Mörsch E. Concrete-steel construction[M]. E. P . Goodrich, translator, McGraw-Hill, New York, 1909. Ritter W. Die bauweise hennebique[J]. Schweizerische Bauzeitung, 1899, 33(7):59-61.
高墙的正截面受弯承载力
求解思路
普通RC高墙在轴力作用下的正截面受弯承载力采用《高层建筑混凝土结构技术规程》(JGJ3-2020)的方法计算。而配置复材管约束混凝土组件的高墙在计算正截面受弯承载力时,需要在普通RC剪力墙截面上考虑复材管约束混凝土压区的合力作用。
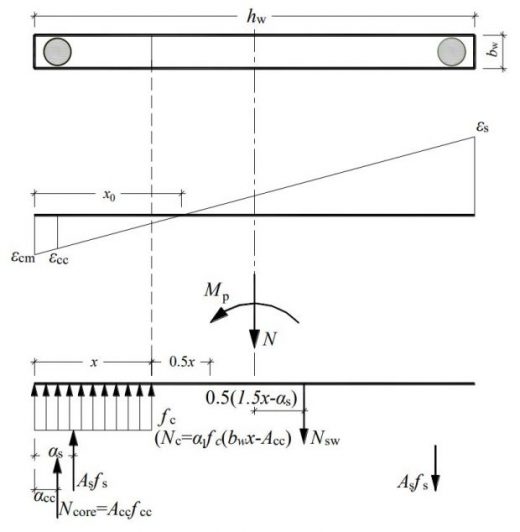
下图为组合墙截面的受力分析模型,计算假定有:
(1)截面变形符合平截面假定;
(2)混凝土的受拉作用不予考虑;
(3)受压区混凝土的应力按矩形应力图等效;
(4)墙截面端部的竖向受拉、受压钢筋屈服;
(5)不考虑墙受压侧距边缘1.5x(1.5倍受压区高度)范围内竖向分布筋的作用,该范围之外的竖向分布筋按受拉屈服考虑。
受力分析模型简图
输入参数
计算公式
组合高墙受压区高度计算公式
$$x=\frac{N+\alpha_{1}f_{c}A_{cc}-N_{core}+h_{wo}b_{w}f_{yw}\rho_{w}}{\alpha_{1}f_{c}b_{w}+1.5b_{w}f_{yw}\rho_{w}}$$组合高墙的平衡方程
$$N=N_c+N_{core}-N_{sw}$$ $$复材管约束混凝土组件压区合力作用:N_{core}=A_{cc}f_{cc}$$ $$混凝土受压提供的反力:N_{c}=\alpha_{1}f_{c}^{'}(b_{w}x-A_{cc})$$ $$墙板内竖向分布筋受拉提供的反力:N_{sw}=(h_{wo}-1.5x)b_{w}f_{yw}\rho_{w}$$受弯承载力计算方程
$$M_{p}=0.5N_{c}(h_{w}-x)+0.5N_{core}(h_{w}-2\alpha_{cc})+A_{s}f_{y}(h_{w}-2\alpha_{s})+0.5N_{sw}(1.5x-\alpha_{s})$$矮墙的斜截面受剪承载力
求解思路
根据钢管混凝土叠合柱结构计算规程(CECS188-2005),钢管混凝土组合剪力墙的斜截面抗承载由几个部分的抗剪贡献叠加而成,抗剪部分一般为管外混凝土、轴力、抗剪钢筋以及钢管等。参考规程中钢管混凝土组合剪力墙斜截面抗剪计算公式,我们提出了配置复材管约束芯柱的矩形截面矮墙抗剪承载力计算公式。
复材管约束芯柱的矩形截面矮墙抗剪承载力计算公式
$$V=\frac{1}{\lambda-0.5}(0.5f_{t}A_{c}+0.13N)+f_{yh}\frac{A_{sh}}{s}h_{wo}+0.1nV_{cal}$$ $$V_{cal}=V_{c}+V_{f}+V_{s}$$ $$V_{c}=\frac{1.75}{\lambda+1}0.704f_{t}D^2 V_{f}=\frac{C_{1}}{\lambda+C_{2}}πtDf_{±\alpha}(C_{3}sin\alpha+C_{4}cos\alpha)sin\alpha V_{s}=\frac{0.276\sqrt{\frac{f_{c}}{19.1}}}{\lambda+0.66}d_{s}^2\sqrt{f_{c}f_{y}}$$其中:Vcal为FCCC-R的总受剪承载力,Vc为填充材料的受剪承载力贡献,Vf为复材管的贡献,Vs为内嵌钢筋的贡献。
注意:在计算Vf时涉及到的C1、C2、C3、C4为待定参数,通过实验数据回归给出。在本课题组实验中,C1=2.34、C2=0.3、C3=0.15、C4=0.5。